方向向量转换为位姿

最近想让机械臂末端沿着物体表面的法向走，这就需要将一个向量 $\vec n = (n_x, n_y, n_z)$ 转为位姿 —— 一个欧式变换4x4的矩阵。

在三维空间中，我们只需要两个角度便可以定义一个方向——该方向与任意两个轴的夹角。

首先将向量 $\vec n$转化为欧拉角(current frame) $rpy=(yaw, pitch, roll)$，其实就是将基坐标系的某一个轴转到与向量共线。

向量转化为欧拉角

可以将X轴、Y轴或是Z轴转到与向量共线，因为我是要机械臂末端对准法向，所以需要Z轴与向量共线。下面我会讲旋转Z轴和旋转X轴的计算。

旋转Z轴

旋转Z轴只用到pitch和roll，也就是先绕Y轴旋转，再绕旋转后的X轴旋转。

将 $\vec n$向xz平面投影得到点$P(n_x,n_z)$ ，可以计算得到 $pitch: \beta =atan2(n_x,n_z) , roll: \alpha = atan2(-n_y, \sqrt{n_x^2+n_z^2})$

算第二个旋转角时要注意，因为 $\sqrt{n_x^2+n_z^2}$ 丢失了符号，所以要根据旋转方向确定符号，我是画图判断的。

$rpy=(0,\beta,\alpha)$

旋转X轴

旋转X轴只用到yaw和pitch，也就是先绕Z轴旋转，再绕Y轴旋转。 $yaw: \gamma =atan2(n_y,n_x),\\ pitch: \beta =atan2(-n_z, \sqrt{n_x^2+n_y^2})$

$rpy=(\gamma, \beta,0)$

欧拉角转四元数

四元数表示顺序$q=[w,x,y,z]$

绕Z轴旋转，yaw $q_z(\gamma)=[cos{\gamma \over 2}, 0,0,sin{\gamma \over 2}]$

绕Y轴旋转， pitch $q_y(\beta)=[cos{\gamma \over 2}，0，sin{\gamma \over 2}, 0]$

绕X轴旋转，roll

\[q_x(\alpha)=[cos{\gamma \over 2}，sin{\gamma \over 2},0,0]\]

总的rpy旋转变换(用 $c\theta$ 表示 $cos{\theta \over 2}$ )

\[q_z(\gamma)q_y(\beta)q_z(\alpha)=\begin{bmatrix} c\gamma \cdot c\beta \cdot c\alpha + s\gamma \cdot s\beta \cdot s\alpha \\ c\gamma \cdot c\beta \cdot s\alpha - s\gamma \cdot s\beta \cdot c\alpha \\ c\gamma \cdot s\beta \cdot c\alpha + s\gamma \cdot c\beta \cdot s\alpha \\ -c\gamma \cdot s\beta \cdot s\alpha + s\gamma \cdot c\beta \cdot c\alpha \end{bmatrix}\]

把上面计算出来的欧拉角带入就可以求出向量到四元数的转换啦。

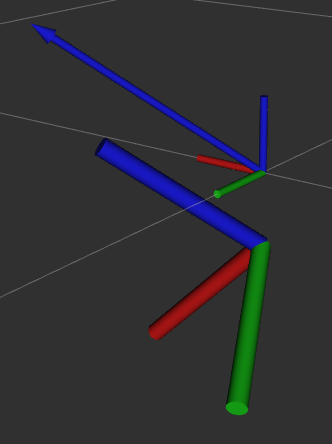
在rviz中验证一下，蓝色的箭头是向量，下面大的坐标系就是经过变换后的坐标系（做了一个向下平移以便与基坐标系区分），可以看到坐标系的Z轴是与向量同向的。