MDH 与 SDH 参数法对比
DH (Denavit- Hartenberg) 法在matlab robotics toolbox中有SDH和MDH之分。
我先看的Craig的书,我自己一般习惯用MDH,但是后来上课的时候又是讲的SDH法,整得我很分裂,现在看Bruno Siciliano的Robotics也是用的SDH法,两种DH参数法用起来容易混,在这里进行一下区分。
其实两种方法的区别主要在于{0}的选择,从而导致了后面坐标系的小区别,link parameters的意义都是相同的。 两种方法大同小异,结果都是相同的,凭个人喜好选择即可。
Modified DH (MDH)

这种DH法是John J. Craig. Introduction to Robotics: Mechanics and Control 上面讲的。他自己也说这个方法和别的书不太一样,所以可能才叫Modified DH吧?
Note that many related conventions go by the name Denavit–Hartenberg, but differ in a few details. For example, the version used in this book differs from some of the robotic literature in the manner of frame numbering. Unlike some other conventions, in this book frame {i} is attached to link i and has its origin lying on joint axis i.
Link parameters表示frame{i-1}到frame{i}的变换$T_{i-1}^i$。从base{0}开始到6轴{6}结束,也可以到工具坐标系{T}结束。
Rules of link-frame attachment
以6轴机械臂为例,Frame {i} 由{i}和{i+1}确定(i=0, 1, 2, 3, 4, 5),下面是确定 frame {i}的步骤。
- 确定Z轴。确定各关节轴线(Axis 1~6),每个轴线对应一个Z轴,比如 axis 1 对应$Z_1$, axis 6 对应$Z_6$。
- 确定原点。要根据相邻的两个Z轴$Z_i$和$Z_{i+1}$确定$O_i$。
- 如果$Z_i$ intersects with $Z_{i+1}$, assign $O_i$ at the point of intersection.
- 如果$Z_i$和$Z_{i+1}$不相交(异面、平行),那么$O_i$ at the point where the common perpendicular meets $Z_i$。
- 确定X轴。X轴的确定也和上面原点的确定类似,需要根据相邻两Z轴的情况来确定。
- 如果相交,那么$X_i$沿两轴相交形成的平面的垂线,$\vec X_i=\vec Z_i\times \vec Z_{i+1}$
- 如果不想交,$X_i$沿公垂线。
根据上述规则确定了frame{1} ~ {6},我们可以把frame {0}设为与{1}重合,以便让尽可能多的DH参数为0。确定了{0}~{6}之后,便可以写DH参数了。
注意{6}并不是工具坐标系{T},而是6轴所在的坐标系,可以再加一个{6} -> {T}的DH参数。
Link parameters
| DH parameters | 意义 |
|---|---|
| $a_i$ | $Z_{i-1}$沿$X_i$到$Z_i$的空间距离 |
| $\alpha_i$ | 以$X_{i-1}$为轴由$Z_{i-1}$到$Z_i$转过的角度 |
| $d_i$ | 由$X_{i-1}$沿$Z_i$到$X_i$的空间距离 |
| $\theta_i$ | 以$Z_i$为轴由$X_{i-1}$到$X_i$转过的角度 |
下面是{i}到{i+1}的变换矩阵 \(T_i^{i+1} = \begin{bmatrix} cos\theta & -sin\theta & 0 & a \\ sin\theta cos\alpha & cos\theta cos\alpha & -sin\alpha & -dsin\alpha \\ sin\theta sin\alpha & cos\theta sin\alpha & cos\alpha & dcos\alpha \\ 0 & 0 & 0 & 1 \end{bmatrix}\)
Standard DH (SDH)

这个方法是Bruno Siciliano. Robotics Modelling, Planning and Control 里面讲的。因为两种方法其实很相似,SDH我就不讲太详细了。
- 确定Z轴。i+1 轴确定$Z_i$
- $O_i$在$Z_{i-1}$和$Z_i$的公垂线与$Z_i$的交点
- $X_i$沿$Z_{i-1}$和$Z_i$公垂线,由i轴指向i+1轴。
下面是{i}到{i+1}的变换矩阵 \(T_i^{i+1} = \begin{bmatrix} cos\theta & -cos\alpha sin\theta & sin\alpha sin\theta & acos\theta \\ sin\theta & cos\theta cos\alpha & -sin\alpha cos\theta & -asin\theta \\ 0 & sin\alpha & cos\alpha & d \\ 0 & 0 & 0 & 1 \end{bmatrix}\)
案例:Anthropomorphic arm 拟人臂
SDH方法建模
我直接从Bruno Siciliano的书上截下来了一页。
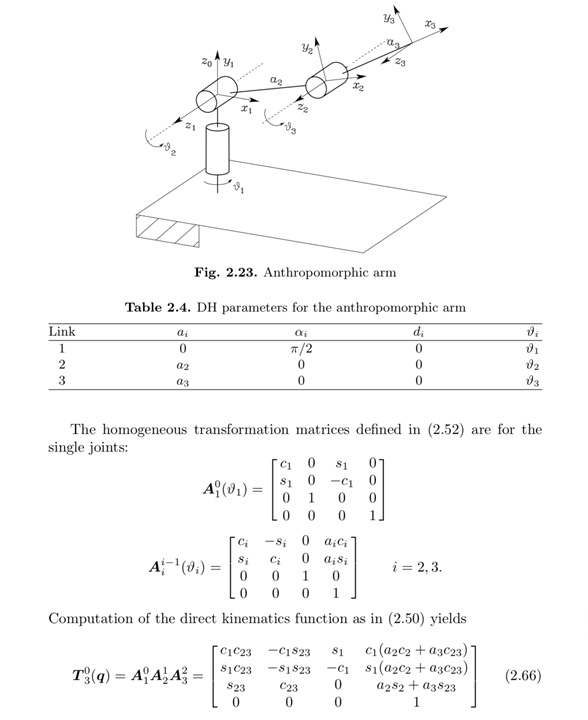
MDH方法建模
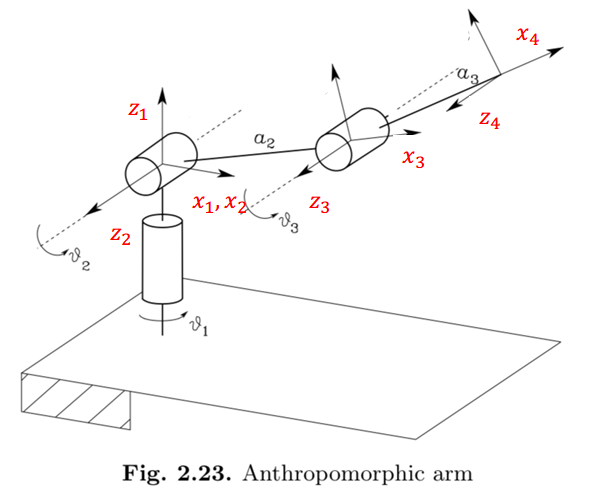
| DH parameter | a | $\alpha$ | d | $\theta$ |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | $v_1$ |
| 2 | 0 | $\pi/2$ | 0 | $v_2$ |
| 3 | $a_2$ | 0 | 0 | $v_3$ |
| 4 | $a_3$ | 0 | 0 | 0 |
第4组其实是到末端单独的一组变换,这样算出来结果跟SDH法是相同的
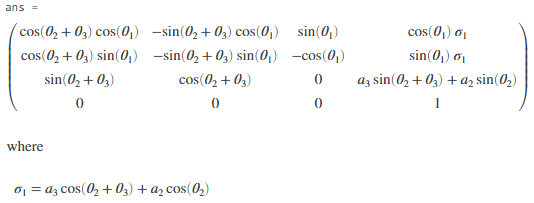
通过对比可以发现,SDH比MDH领先一个轴,主要是因为MDH的{0}与{1}是重合的,而SDH的{0}是1轴,{1}是2轴,所以形式上SDH更加简洁一点点。